99 - Reference

Source: vignettes/a99-reference.Rmd

Quick start 

x <- symbol('x')
as.character(x)
#> [1] "x"
x
#> c: x
as_expr(x)
#> expression(x)
2*x
#> c: 2⋅x
y <- symbol('y')
sqrt(3*x^y)
#> c:       ____
#>         ╱  y 
#>    √3⋅╲╱  x
z <- cos(x)^2 + sin(x)^2
z
#> c:    2         2   
#>    sin (x) + cos (x)
simplify(z)
#> c: 1
tex(z)
#> [1] "\\sin^{2}{\\left(x \\right)} + \\cos^{2}{\\left(x \\right)}"
z <- cos(x)*cos(y) - sin(x)*sin(y)
z
#> c: -sin(x)⋅sin(y) + cos(x)⋅cos(y)
simplify(z)
#> c: cos(x + y)
z <- cos(x + y)
z
#> c: cos(x + y)
expand(z)
#> c: cos(x + y)
expand_trig(z)
#> c: -sin(x)⋅sin(y) + cos(x)⋅cos(y)
x <- symbol('x')
y <- symbol('y')
z <- log(x*y)
z
#> c: log(x⋅y)
expand_log(z)
#> c: log(x) + log(y)

Sums 

x <- symbol("x")
sum_(1/x, "x", 1, 10)
#> c: 7381
#>    ────
#>    2520
sum_(1/x, x, 1, 10)
#> c: 7381
#>    ────
#>    2520
s <- sum_(1/x, "x", 1, 10)
as_expr(s)
#> [1] 2.928968
sum(1/(1:10))
#> [1] 2.928968
n <- symbol("n")
simplify(sum_(x, x, 1, n))
#> c: n⋅(n + 1)
#>    ─────────
#>        2

Products 

x <- symbol("x")
p <- prod_(1/x, "x", 1, 10)
p
#> c: 1/3628800
as_expr(p)
#> [1] 2.755732e-07
prod(1/(1:10))
#> [1] 2.755732e-07
n <- symbol("n")
prod_(x, x, 1, n)
#> c: n!

Integrals 

x <- symbol("x")

int(1/x, x, 1, 10)
#> c: log(10)
i1 <- int(1/x, x, 1, 10, doit = FALSE)
i1
#> c: 10     
#>    ⌠      
#>    ⎮  1   
#>    ⎮  ─ dx
#>    ⎮  x   
#>    ⌡      
#>    1
tex(i1)
#> [1] "\\int\\limits_{1}^{10} \\frac{1}{x}\\, dx"
doit(i1)
#> c: log(10)
int(1/x, x)
#> c: log(x)
i1 <- int(1/x, x, doit = FALSE)
i1
#> c: ⌠     
#>    ⎮ 1   
#>    ⎮ ─ dx
#>    ⎮ x   
#>    ⌡
tex(i1)
#> [1] "\\int \\frac{1}{x}\\, dx"
doit(i1)
#> c: log(x)

Limits 

x <- symbol("x")
lim(sin(x)/x, "x", 0)
#> c: 1
lim(1/x, "x", 0, dir = '+')
#> c: ∞
lim(1/x, "x", 0, dir = '-')
#> c: -∞

We can also postpone evaluation:

x <- symbol("x")
lim(sin(x)/x, "x", 0)
#> c: 1
lim(sin(x)/x, x, 0)
#> c: 1
res <- lim(sin(x)/x, "x", 0, doit = FALSE)
res
#> c:      ⎛sin(x)⎞
#>     lim ⎜──────⎟
#>    x─→0⁺⎝  x   ⎠
as.character(res)
#> [1] "Limit(sin(x)/x, x, 0, dir='+')"
tex(res)
#> [1] "\\lim_{x \\to 0^+}\\left(\\frac{\\sin{\\left(x \\right)}}{x}\\right)"
doit(res)
#> c: 1
as_expr(res)
#> [1] 1

Derivatives

Note that the function is called d() and not deriv().

x <- symbol("x")
y <- symbol("y")
f <- 3*x^2 + x*y^2
f
#> c:    2      2
#>    3⋅x  + x⋅y
as_expr(f)
#> expression(3 * x^2 + x * y^2)
der(f, "x")
#> c:        2
#>    6⋅x + y
der(f, x)
#> c:        2
#>    6⋅x + y
der(f, c("x", "y"))
#> c: ⎡       2       ⎤
#>    ⎣6⋅x + y   2⋅x⋅y⎦
der(f, list(x, y))
#> c: ⎡       2       ⎤
#>    ⎣6⋅x + y   2⋅x⋅y⎦
f1 <- der(f, list(x, y))
f1
#> c: ⎡       2       ⎤
#>    ⎣6⋅x + y   2⋅x⋅y⎦
as.character(f1)
#> [1] "[6*x + y^2, 2*x*y]"
as_expr(f1)
#> expression(cbind(6 * x + y^2, 2 * x * y))
eval(as_expr(f1), list(x = 1, y = 2))
#>      [,1] [,2]
#> [1,]   10    4
der(f1, list(x, y))
#> c: ⎡ 6   2⋅y⎤
#>    ⎢        ⎥
#>    ⎣2⋅y  2⋅x⎦
f2 <- der2(f, list(x, y))
f2
#> c: ⎡ 6   2⋅y⎤
#>    ⎢        ⎥
#>    ⎣2⋅y  2⋅x⎦
as_expr(f2)
#> expression(matrix(c(6, 2 * y, 2 * y, 2 * x), nrow = 2))
eval(as_expr(f2), list(x = 1, y = 2))
#>      [,1] [,2]
#> [1,]    6    4
#> [2,]    4    2
x <- symbol("x")
y <- symbol("y")
f <- eval_to_symbol("[3*x**2 + x*y**2, 2*x, 5*y]")
f
#> c: ⎡   2      2          ⎤
#>    ⎣3⋅x  + x⋅y , 2⋅x, 5⋅y⎦
der(f, list(x, y))
#> c: ⎡       2      ⎤
#>    ⎢6⋅x + y   2  0⎥
#>    ⎢              ⎥
#>    ⎣ 2⋅x⋅y    0  5⎦

Taylor expansion 

def_sym(x)
f <- cos(x)
ft_with_O <- taylor(f, x0 = 0, n = 4+1)
ft_with_O
#> c:      2    4          
#>        x    x     ⎛ 5.0⎞
#>    1 - ── + ── + O⎝x   ⎠
#>        2    24
ft_with_O %>% drop_remainder() %>% as_expr()
#> expression(x^4/24 - x^2/2 + 1)

Linear algebra 

A <- matrix(c("x", 0, 0, "2*x"), 2, 2)
A
#>      [,1] [,2] 
#> [1,] "x"  "0"  
#> [2,] "0"  "2*x"
B <- as_sym(A)
B
#> c: ⎡x   0 ⎤
#>    ⎢      ⎥
#>    ⎣0  2⋅x⎦
2*B
#> c: ⎡2⋅x   0 ⎤
#>    ⎢        ⎥
#>    ⎣ 0   4⋅x⎦
B*B # Component-wise / Hadamard product
#> c: ⎡ 2      ⎤
#>    ⎢x    0  ⎥
#>    ⎢        ⎥
#>    ⎢       2⎥
#>    ⎣0   4⋅x ⎦
dim(B)
#> [1] 2 2
sqrt(B)
#> c: ⎡√x    0  ⎤
#>    ⎢         ⎥
#>    ⎣0   √2⋅√x⎦
log(B)
#> c: ⎡log(x)    zoo   ⎤
#>    ⎢                ⎥
#>    ⎣ zoo    log(2⋅x)⎦
sum(B)
#> c: 3⋅x
B %*% t(B)
#> c: ⎡ 2      ⎤
#>    ⎢x    0  ⎥
#>    ⎢        ⎥
#>    ⎢       2⎥
#>    ⎣0   4⋅x ⎦
diag(B)
#> c: [x  2⋅x]
cbind(B, B)
#> c: ⎡x   0   x   0 ⎤
#>    ⎢              ⎥
#>    ⎣0  2⋅x  0  2⋅x⎦
rbind(B, B)
#> c: ⎡x   0 ⎤
#>    ⎢      ⎥
#>    ⎢0  2⋅x⎥
#>    ⎢      ⎥
#>    ⎢x   0 ⎥
#>    ⎢      ⎥
#>    ⎣0  2⋅x⎦
det(B)
#> c:    2
#>    2⋅x
QRdecomposition(B)
#> $Q
#> c: ⎡ x      ⎤
#>    ⎢───   0 ⎥
#>    ⎢│x│     ⎥
#>    ⎢        ⎥
#>    ⎢      x ⎥
#>    ⎢ 0   ───⎥
#>    ⎣     │x│⎦
#> 
#> $R
#> c: ⎡│x│    0  ⎤
#>    ⎢          ⎥
#>    ⎣ 0   2⋅│x│⎦
A <- matrix(c("a", 0, 0, 0, "a", "a", "a", 0, 0), 3, 3)
B <- as_sym(A)
eigenval(B)
#> [[1]]
#> [[1]]$eigval
#> c: a
#> 
#> [[1]]$eigmult
#> [1] 2
#> 
#> 
#> [[2]]
#> [[2]]$eigval
#> c: 0
#> 
#> [[2]]$eigmult
#> [1] 1
eigenvec(B)
#> [[1]]
#> [[1]]$eigval
#> c: 0
#> 
#> [[1]]$eigmult
#> [1] 1
#> 
#> [[1]]$eigvec
#> c: [-1  0  1]ᵀ
#> 
#> 
#> [[2]]
#> [[2]]$eigval
#> c: a
#> 
#> [[2]]$eigmult
#> [1] 2
#> 
#> [[2]]$eigvec
#> c: [1  0  0]ᵀ
eigen(eval(as_expr(B), list(a = 2)))
#> eigen() decomposition
#> $values
#> [1] 2 2 0
#> 
#> $vectors
#>      [,1]          [,2]       [,3]
#> [1,]    1 -1.000000e+00 -0.7071068
#> [2,]    0  2.220446e-16  0.0000000
#> [3,]    0  2.220446e-16  0.7071068
B
#> c: ⎡a  0  a⎤
#>    ⎢       ⎥
#>    ⎢0  a  0⎥
#>    ⎢       ⎥
#>    ⎣0  a  0⎦
diag(B)
#> c: [a  a  0]
diag(B) <- "b"
B
#> c: ⎡b  0  a⎤
#>    ⎢       ⎥
#>    ⎢0  b  0⎥
#>    ⎢       ⎥
#>    ⎣0  a  b⎦
diag(B)[-2] <- "a"
B
#> c: ⎡a  0  a⎤
#>    ⎢       ⎥
#>    ⎢0  b  0⎥
#>    ⎢       ⎥
#>    ⎣0  a  a⎦

Solve

Below find an example with maximising the multinomial likelihood.

p <- as_sym(paste0("p", 1:3))
y <- as_sym(paste0("y", 1:3))
a <- as_sym("a")
l <- sum(y*log(p))
l
#> c: y₁⋅log(p₁) + y₂⋅log(p₂) + y₃⋅log(p₃)
L <- -l + a*(sum(p) - 1)
L
#> c: a⋅(p₁ + p₂ + p₃ - 1) - y₁⋅log(p₁) - y₂⋅log(p₂) - y₃⋅log(p₃)
tex(L)
#> [1] "a \\left(p_{1} + p_{2} + p_{3} - 1\\right) - y_{1} \\log{\\left(p_{1} \\right)} - y_{2} \\log{\\left(p_{2} \\right)} - y_{3} \\log{\\left(p_{3} \\right)}"
g <- der(L, list(p, a))
g
#> c: ⎡    y₁      y₂      y₃                  ⎤
#>    ⎢a - ──  a - ──  a - ──  p₁ + p₂ + p₃ - 1⎥
#>    ⎣    p₁      p₂      p₃                  ⎦
sol <- solve_sys(g, list(p, a))
sol
#> Solution 1:
#>   a  =  y₁ + y₂ + y₃ 
#>   p1 =       y₁     
#>        ────────────
#>        y₁ + y₂ + y₃ 
#>   p2 =       y₂     
#>        ────────────
#>        y₁ + y₂ + y₃ 
#>   p3 =       y₃     
#>        ────────────
#>        y₁ + y₂ + y₃
sol[[1L]]$p1
#> c:      y₁     
#>    ────────────
#>    y₁ + y₂ + y₃
tex(sol[[1L]]$p1)
#> [1] "\\frac{y_{1}}{y_{1} + y_{2} + y_{3}}"

Assumptions 

x <- symbol("x", positive = TRUE)
solve_sys(x^2 - 1, 0, x)
#> x = 1

x <- symbol("x", real = TRUE)
solve_sys(x^2 + 1, 0, x)
#> No solutions

x <- symbol("x")
solve_sys(x^2 + 1, 0, x)
#> x = -ⅈ
#> x = ⅈ

Substitution 

x <- symbol('x')
eq <- 2*x^2 - x
eq
#> c:    2    
#>    2⋅x  - x
subs(eq, x, "y")
#> c:    2    
#>    2⋅y  - y
p <- as_sym(paste0("p", 1:3))
y <- as_sym(paste0("y", 1:3))
a <- as_sym("a")
l <- sum(y*log(p))
L <- -l + a*(sum(p) - 1)
g <- der(L, c(a, p))
sols <- solve_sys(g, list(a, p))
sol <- sols[[1L]]
sol
#> $a
#> c: y₁ + y₂ + y₃
#> 
#> $p1
#> c:      y₁     
#>    ────────────
#>    y₁ + y₂ + y₃
#> 
#> $p2
#> c:      y₂     
#>    ────────────
#>    y₁ + y₂ + y₃
#> 
#> $p3
#> c:      y₃     
#>    ────────────
#>    y₁ + y₂ + y₃
H <- der2(L, list(p, a))
H
#> c: ⎡ y₁             ⎤
#>    ⎢───   0    0   1⎥
#>    ⎢  2             ⎥
#>    ⎢p₁              ⎥
#>    ⎢                ⎥
#>    ⎢      y₂        ⎥
#>    ⎢ 0   ───   0   1⎥
#>    ⎢       2        ⎥
#>    ⎢     p₂         ⎥
#>    ⎢                ⎥
#>    ⎢           y₃   ⎥
#>    ⎢ 0    0   ───  1⎥
#>    ⎢            2   ⎥
#>    ⎢          p₃    ⎥
#>    ⎢                ⎥
#>    ⎣ 1    1    1   0⎦
H_sol <- subs(H, sol)
H_sol
#> c: ⎡              2                                     ⎤
#>    ⎢(y₁ + y₂ + y₃)                                      ⎥
#>    ⎢───────────────         0                0         1⎥
#>    ⎢       y₁                                           ⎥
#>    ⎢                                                    ⎥
#>    ⎢                               2                    ⎥
#>    ⎢                 (y₁ + y₂ + y₃)                     ⎥
#>    ⎢       0         ───────────────         0         1⎥
#>    ⎢                        y₂                          ⎥
#>    ⎢                                                    ⎥
#>    ⎢                                                2   ⎥
#>    ⎢                                  (y₁ + y₂ + y₃)    ⎥
#>    ⎢       0                0         ───────────────  1⎥
#>    ⎢                                         y₃         ⎥
#>    ⎢                                                    ⎥
#>    ⎣       1                1                1         0⎦

Subsetting

Note that all vectors in caracas are column vectors.

A <- matrix(c("a", 0, 0, 0, "a", "a", "a", 0, 0), 3, 3)
B <- as_sym(A)
B[, 2]
#> c: [0  a  a]ᵀ
B[, -2]
#> c: ⎡a  a⎤
#>    ⎢    ⎥
#>    ⎢0  0⎥
#>    ⎢    ⎥
#>    ⎣0  0⎦
B[1, ]
#> c: [a  0  a]ᵀ
B[1, , drop = FALSE] # Note this is a 1x3 matrix
#> c: [a  0  a]
B[, 2] <- "x"
B
#> c: ⎡a  x  a⎤
#>    ⎢       ⎥
#>    ⎢0  x  0⎥
#>    ⎢       ⎥
#>    ⎣0  x  0⎦

Interactively show \(\LaTeX\) representation

plots the following in the plot window:

You can also provide a string instead:

texshow(paste0("B = ", tex(B)))

giving

texshow(paste0("B = ", tex(B)))

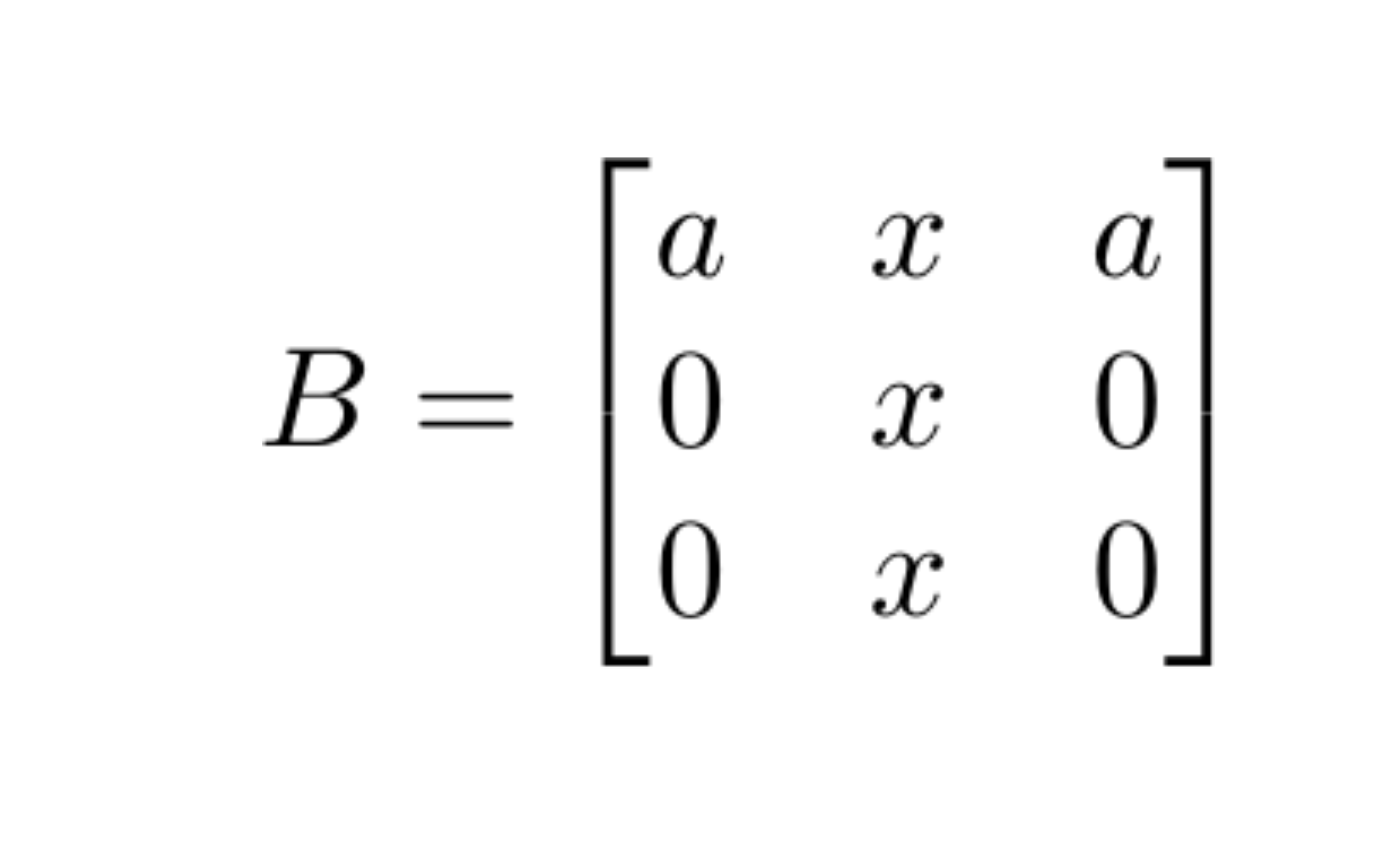
Using SymPy directly 

sympy <- get_sympy()
sympy$diff("2*a*x", "x")
#> 2*a
sympy$solve("x**2 - 1", "x")
#> [[1]]
#> -1
#> 
#> [[2]]
#> 1

Assumptions

Below we give a brief example of assumptions. First consider the Cholesky decomposition of a matrix:

A <- matrix(c("x+1", 1, 1, 1), 2, 2) %>% as_sym()
A
#> c: ⎡x + 1  1⎤
#>    ⎢        ⎥
#>    ⎣  1    1⎦
do_la(A, "cholesky")
#> Matrix must be Hermitian.

This fails as A is not positive (semi-)definite.

To ensure this, we need to impose restrictions on x. This is done by defining a symbol with an assumption about positivity:

y <- symbol("y", positive = TRUE)

We continue and define B, where it is important that declare_symbols = FALSE or else a new y will automatically be defined by caracas overwriting the above definition:

B <- as_sym("[[y + 1, 1], [1, 1]]", declare_symbols = FALSE)
B
#> c: ⎡y + 1  1⎤
#>    ⎢        ⎥
#>    ⎣  1    1⎦
do_la(B, "cholesky")
#> c: ⎡  _______                 ⎤
#>    ⎢╲╱ y + 1          0       ⎥
#>    ⎢                          ⎥
#>    ⎢               ___________⎥
#>    ⎢    1         ╱       1   ⎥
#>    ⎢─────────    ╱  1 - ───── ⎥
#>    ⎢  _______  ╲╱       y + 1 ⎥
#>    ⎣╲╱ y + 1                  ⎦

It is possible to ask for properties (see https://docs.sympy.org/latest/modules/assumptions/ask.html):

ask(y, "positive")
#> [1] TRUE
ask(B, "hermitian")
#> [1] TRUE
ask(A, "hermitian")
#> [1] NA

Output 

# Multinomial likelihood
p <- as_sym(paste0("p", 1:3))
y <- as_sym(paste0("y", 1:3))
a <- as_sym("a")
l <- sum(y*log(p))
L <- -l + a*(sum(p) - 1)
L
#> c: a⋅(p₁ + p₂ + p₃ - 1) - y₁⋅log(p₁) - y₂⋅log(p₂) - y₃⋅log(p₃)
print(L, ascii = TRUE)
#> c: a⋅(p₁ + p₂ + p₃ - 1) - y₁⋅log(p₁) - y₂⋅log(p₂) - y₃⋅log(p₃)
g <- der(L, list(p, a))
sol <- solve_sys(g, list(p, a))
sol
#> Solution 1:
#>   a  =  y₁ + y₂ + y₃ 
#>   p1 =       y₁     
#>        ────────────
#>        y₁ + y₂ + y₃ 
#>   p2 =       y₂     
#>        ────────────
#>        y₁ + y₂ + y₃ 
#>   p3 =       y₃     
#>        ────────────
#>        y₁ + y₂ + y₃
print(sol, simplify = FALSE)
#> [[1]]
#> [[1]]$a
#> c: y₁ + y₂ + y₃
#> 
#> [[1]]$p1
#> c:      y₁     
#>    ────────────
#>    y₁ + y₂ + y₃
#> 
#> [[1]]$p2
#> c:      y₂     
#>    ────────────
#>    y₁ + y₂ + y₃
#> 
#> [[1]]$p3
#> c:      y₃     
#>    ────────────
#>    y₁ + y₂ + y₃
as.character(g)
#> [1] "[a - y1/p1, a - y2/p2, a - y3/p3, p1 + p2 + p3 - 1]"
as_character_matrix(g)
#>      [,1]        [,2]        [,3]        [,4]              
#> [1,] "a - y1/p1" "a - y2/p2" "a - y3/p3" "p1 + p2 + p3 - 1"

Options

The following options are available:

  • caracas.print.method (utf8 is default, others are: prettyascii, ascii, compactascii)
  • caracas.print.rowvec
  • caracas.print.sol.simplify
sol
#> Solution 1:
#>   a  =  y₁ + y₂ + y₃ 
#>   p1 =       y₁     
#>        ────────────
#>        y₁ + y₂ + y₃ 
#>   p2 =       y₂     
#>        ────────────
#>        y₁ + y₂ + y₃ 
#>   p3 =       y₃     
#>        ────────────
#>        y₁ + y₂ + y₃
L
#> c: a⋅(p₁ + p₂ + p₃ - 1) - y₁⋅log(p₁) - y₂⋅log(p₂) - y₃⋅log(p₃)
options(caracas.print.method = "prettyascii") 
sol
#> Solution 1:
#>   a  =  y1 + y2 + y3 
#>   p1 =       y1     
#>        ------------
#>        y1 + y2 + y3 
#>   p2 =       y2     
#>        ------------
#>        y1 + y2 + y3 
#>   p3 =       y3     
#>        ------------
#>        y1 + y2 + y3
L
#> c: a*(p1 + p2 + p3 - 1) - y1*log(p1) - y2*log(p2) - y3*log(p3)
options(caracas.print.method = "ascii") 
sol
#> Solution 1:
#>   a  =  y1 + y2 + y3 
#>   p1 =  y1/(y1 + y2 + y3) 
#>   p2 =  y2/(y1 + y2 + y3) 
#>   p3 =  y3/(y1 + y2 + y3)
L
#> c: a*(p1 + p2 + p3 - 1) - y1*log(p1) - y2*log(p2) - y3*log(p3)
options(caracas.print.method = NULL) # Or 'utf8' 
sol
#> Solution 1:
#>   a  =  y₁ + y₂ + y₃ 
#>   p1 =       y₁     
#>        ────────────
#>        y₁ + y₂ + y₃ 
#>   p2 =       y₂     
#>        ────────────
#>        y₁ + y₂ + y₃ 
#>   p3 =       y₃     
#>        ────────────
#>        y₁ + y₂ + y₃
L
#> c: a⋅(p₁ + p₂ + p₃ - 1) - y₁⋅log(p₁) - y₂⋅log(p₂) - y₃⋅log(p₃)
p
#> c: [p₁  p₂  p₃]ᵀ
options(caracas.print.rowvec = FALSE)
p
#> c: ⎡p₁⎤
#>    ⎢  ⎥
#>    ⎢p₂⎥
#>    ⎢  ⎥
#>    ⎣p₃⎦
options(caracas.print.rowvec = NULL) # reset to default (TRUE)
sol
#> Solution 1:
#>   a  =  y₁ + y₂ + y₃ 
#>   p1 =       y₁     
#>        ────────────
#>        y₁ + y₂ + y₃ 
#>   p2 =       y₂     
#>        ────────────
#>        y₁ + y₂ + y₃ 
#>   p3 =       y₃     
#>        ────────────
#>        y₁ + y₂ + y₃
options(caracas.print.sol.simplify = FALSE)
sol
#> [[1]]
#> [[1]]$a
#> c: y₁ + y₂ + y₃
#> 
#> [[1]]$p1
#> c:      y₁     
#>    ────────────
#>    y₁ + y₂ + y₃
#> 
#> [[1]]$p2
#> c:      y₂     
#>    ────────────
#>    y₁ + y₂ + y₃
#> 
#> [[1]]$p3
#> c:      y₃     
#>    ────────────
#>    y₁ + y₂ + y₃
options(caracas.print.sol.simplify = NULL) # reset to default (TRUE)